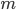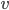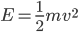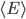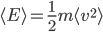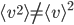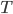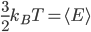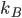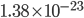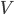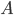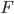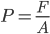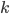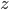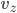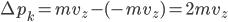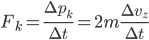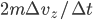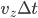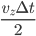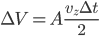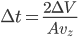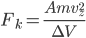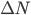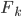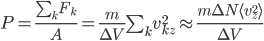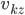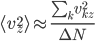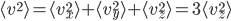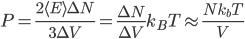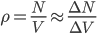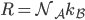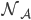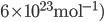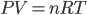Nous savons que tout ce qui nous entoure est fait d'atomes (ou de molécules). Mais si cela nous semble aujourd'hui évident, cela n'a pas toujours été le cas. Il y a eu dès l'Antiquité, des débats passionnés sur la structure de la matière: la matière est-elle continue ou discontinue? Si l'idée d'atome est très ancienne (elle remonte à Leucippe né en 460 avant J.C.) elle n'eut que très peu de succès avant de resurgir avec les travaux de John Dalton en 1808, où la théorie atomique devient scientifique et convainc peu à peu toute la communauté scientifique. Il faut cependant attendre le début du vingtième siècle pour que cette théorie soit solidement établie.
Il y a quelque chose de tout à fait remarquable à propos de la théorie atomique. Comment, au début du dix-neuvième siècle, pouvait-on en arriver à une conclusion aussi remarquable avec les moyens de l'époque? Il existe plusieurs réponses à cela, mais ce qui va nous intéresser ici, c'est le comportement des gaz.
Attention!! Les calculs qui suivent sont volontairement simplifiés, il est donc normal que ces calculs ne soient pas très rigoureux.
Intuitivement, on peut voir un gaz comme un ensemble de particules (atomes ou molécules par exemple) qui interagissent très peu entre-elles. On va dire, pour simplifier, que l'on néglige totalement toutes les interactions entre les particules du gaz: elles se croisent «sans se voir». Si on enferme un gaz dans une cavité, il faut quand même tenir compte de l'interaction entre les particules du gaz et la paroi de la cavité. Les particules du gaz sont en mouvement permanent, quand elles rencontrent une paroi, il y des chocs et donc une certaine pression. La pression d'un gaz est donc le résultat de chocs des particules du gaz sur les parois.
Que peut-on dire sur la vitesse des particules du gaz? Une particule de gaz de masse 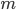 et de vitesse
et de vitesse 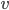 , possède une énergie cinétique donnée par:
, possède une énergie cinétique donnée par:
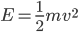
Étant donné le très grand nombre de particules dans un gaz, on ne peut pas prendre note de l'énergie cinétique de chaque particules séparément. On va donc s'intéresser à leur énergie cinétique moyenne que l'on va noter 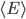 . On a bien sûr:
. On a bien sûr: 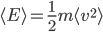 . Attention que
. Attention que 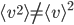 , c'est à dire que la moyenne des carrés n'est pas égale au carré de la moyenne.
, c'est à dire que la moyenne des carrés n'est pas égale au carré de la moyenne.
Peut-on relier cette énergie moyenne à une quantité mesurable? La réponse est oui, elle est liée à la température 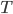 . On a en fait:
. On a en fait:
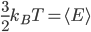
où 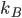 est une constante, appelée constante de Boltzmann, et qui vaut
est une constante, appelée constante de Boltzmann, et qui vaut 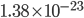 joules par kelvin. Discuter de la signification précise de cette constante nous entraînerait trop loin, ce qui est important ici c'est que la température est une mesure de l'énergie cinétique moyenne des particules du gaz.
joules par kelvin. Discuter de la signification précise de cette constante nous entraînerait trop loin, ce qui est important ici c'est que la température est une mesure de l'énergie cinétique moyenne des particules du gaz.
Supposons donc un gaz enfermé dans un certain volume 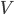 . La pression du gaz est supposé constante sur toute la surface de la cavité. Choisissons une petite surface
. La pression du gaz est supposé constante sur toute la surface de la cavité. Choisissons une petite surface 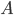 sur la cavité où l'on va mesure la pression. Si
sur la cavité où l'on va mesure la pression. Si 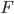 est la force exercée par le gaz sur la surface
est la force exercée par le gaz sur la surface 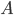 , on a:
, on a:
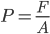
Considérons donc une particule 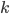 qui frappe la surface
qui frappe la surface 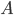 . Mettons l'axe
. Mettons l'axe 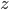 perpendiculaire à la surface (l'axe
perpendiculaire à la surface (l'axe 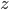 est horizontal sur la figure qui suit), si on note
est horizontal sur la figure qui suit), si on note 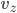 la composante suivant
la composante suivant 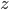 de la vitesse de la particule, alors elle transmet une quantité de mouvement:
de la vitesse de la particule, alors elle transmet une quantité de mouvement:
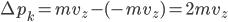
car elle arrive et repart avec la même vitesse. La force est la variation de la quantité de mouvement par rapport au temps, donc:
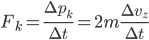
Qu'est ce que  ? Si on modélise l'interaction comme un choc instantané, alors
? Si on modélise l'interaction comme un choc instantané, alors  ne peut pas être le temps réél d'interaction (qui serait infiniment court). Mais il est possible de contourner le problème. On peut très bien choisir un certain
ne peut pas être le temps réél d'interaction (qui serait infiniment court). Mais il est possible de contourner le problème. On peut très bien choisir un certain  (arbitraire), et calculer la force moyenne
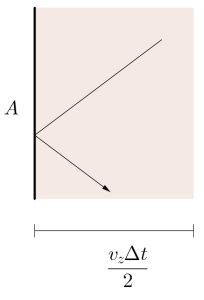
(arbitraire), et calculer la force moyenne 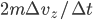 sur ce temps (c'est ce que l'on veut faire de toute façon: une moyenne). Ce temps, on le considère conventionnement comme le temps d'interaction. À ce temps correspond une distance d'interaction, qui est la distance la plus grande à laquelle se trouve la particule de la paroi pendant le temps d'interaction. La distance totale parcourue (i.e. aller et retour) est alors de
sur ce temps (c'est ce que l'on veut faire de toute façon: une moyenne). Ce temps, on le considère conventionnement comme le temps d'interaction. À ce temps correspond une distance d'interaction, qui est la distance la plus grande à laquelle se trouve la particule de la paroi pendant le temps d'interaction. La distance totale parcourue (i.e. aller et retour) est alors de 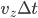 , la distance maximale à la paroi (distance d'interaction) est donc la moitié soit
, la distance maximale à la paroi (distance d'interaction) est donc la moitié soit 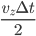 . Cela correspond à un volume d'interaction:
. Cela correspond à un volume d'interaction:
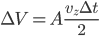
et donc:
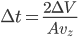
Et la force exercée par la particule 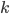 est alors:
est alors:
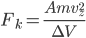
Pendant le temps  , il y a un certains nombre
, il y a un certains nombre 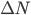 de particules qui interagissent avec la paroi et non une seule. La pression est donc la somme des
de particules qui interagissent avec la paroi et non une seule. La pression est donc la somme des 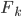 divisée par la surface
divisée par la surface 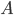 :
:
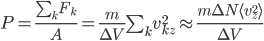
en notant cette fois 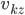 la composante
la composante 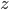 de la vitesse de la particule
de la vitesse de la particule 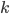 , et en utilisant:
, et en utilisant:
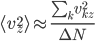
Enfin, on doit avoir, puisqu'il n'y a pas de direction privilégiée:
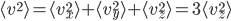
On a donc, en introduisant aussi l'énergie cinétique moyenne, et utilisant la formule qui lie température et énergie cinétique moyenne:
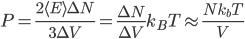
où l'on a utilisé le fait que la densité est constante:
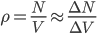
On peut encore poser 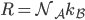 où
où 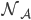 est le nombre d'Avogadro (
est le nombre d'Avogadro (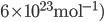 pour travailler en moles (avec
pour travailler en moles (avec 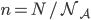 ), on a alors:
), on a alors:
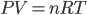
Ceci illustre toute la puissance de l'hypothèse atomique. L'équation que l'on vient de montrer est l'équation des gaz parfaits. On parle de gaz parfait, car contrairement aux gaz rééls, on a supposé qu'il n'y avait aucune interactions entre les particules. L'équation des gaz parfaits se vérifie donc bien à faible densité, plus la densité est grande, plus cette équation est imprécise. Ceci constitue donc une confirmation expérimentale éclatante de la théorie atomique.