Relativité de Galilée

Idée générale

Imaginez. Vous vous retrouvez dans un bateau alors qu'il n'y a pas la moindre houle. Enfermé dans une cale, vous n'avez aucune fenêtre: vous ne pouvez rien savoir de ce qui se passe dehors. La mer étant parfaitement calme, vous ne ressentez aucun mouvement. La question est la suivante: est-il possible, par une quelconque expérience physique de calculer la vitesse du bateau par rapport au rivage? La réponse à cette question mène au principe de relativité.

Dans votre bateau, vous pouvez faire toutes les expériences que vous voulez: observer la chute d'un objet, l'écoulement d'un fluide, des chocs entre des mobiles,... Rien ne pourra vous aider: aucune expérience ne vous dira si votre bateau est immobile ou pas. Quelque soit la vitesse du bateau par rapport au rivage, les expériences les plus précises du monde ne vont serons d'aucune utilité.

Il faut nuancer toutefois. Si le bateau accélère brutalement, vous le sentirez sans problème. De même, si il se trouve dans un virage, vous ressentirez les effets de la force centrifuge. Vous n'aurez toujours aucune idée de sa vitesse, mais vous pourrez mesurer son accélération relativement facilement. Pour ne pas devoir traiter ces cas, on va supposer que le bateau se déplace en ligne droite et que sa vitesse est constante. On dit dans ce cas que le référentiel du bateau est galiléen ou inertiel.

Le principe de relativité exclut l'existence d'un référentiel privilégié par rapport auquel on pourrait calculer sa vitesse (un référentiel au repos absolu). Dire que l'on se déplace à une certaine vitesse n'a de sens qu'en précisant par rapport à quel référentiel cette vitesse est mesurée. Certes, quand nous marchons, on peut dire qu'on se déplace à une certaine vitesse. Mais nous déplaçons nous par rapport à la terre ou la terre se déplace t elle par rapport à nous? Galilée affirme qu'il n'y a aucune raison de choisir l'une ou l'autre de ces affirmations.

Cela se traduit par les équations qui permettent de passer d'un référentiel à l'autre. Elles montrent que les lois de la physique sont les mêmes pour tout les référentiels galiléens. Dans ce cas, le principe vu plus haut se justifie.

Transformations de Galilée

Prenons donc 2 référentiels, $R$ et $R\prime$ en mouvement par rapport à l'autre à la vitesse $v$ (vitesse constante).

Le référentiel $R$ a pour origine $O$ et les axes $x$, $y$ et $z$, et le référentiel $R\prime$ a l'origine $O\prime$ et les axes $x\prime$, $y\prime$ et $z\prime$ (voir figure). On voit que les axes $x$ et $x\prime$ sont alignés pour la simplicité des équations. Imaginons que $O\prime$ s'éloigne de $O$ à la vitesse $v$.Un point $P$ à les coordonnées $x$, $y$ et $z$ dans $R$. Quelles seront ses coordonnées dans $R\prime$?

Calculons d'abord la coordonnée $x\prime$:

Nous savons que $vt$ est la distance entre $O$ et $O\prime$.

c'est donc que (voir schéma ci-dessous qui ne montre que l'axe $x$ $x\prime$):

Déplacer le référentiel suivant l'axe $x$ n'as évidemment pas changer les coordonnées $y$ et $z$:

Enfin, Galilée ajoute:

pour montrer que les coordonnées de temps sont les mêmes dans les 2 référentiels (ex: si un phénomène prend 2 minutes dans un référentiel, il prendra 2 minutes dans l'autre: le temps s'écoule de la même manière dans tous les référentiels). Nous avons donc:

Ces relations s'inversent facilement:

Loi d'addition des vitesses

Voici une conséquence importante:

Un mobile se déplace à la vitesse $v\prime$ dans le référentiel $R\prime$. Quelle est sa vitesse dans un autre référentiel, $R$ se déplaçant à la vitesse $V$ par rapport à $R\prime$?

On calcule sa vitesse dans le référentiel $R$ en calculant simplement la dérivée par rapport au temps:

Car on a évidemment $v\prime =\frac{dx\prime }{dt\prime }$.

Exemple:

Imaginons un train roulant à la vitesse de 20 m/s, et un voyageur se déplaçant dans le couloir du train à 1 m/s, dans le sens de la marche du train. Sa vitesse par rapport à la terre est donc de 20+1=21 m/s.

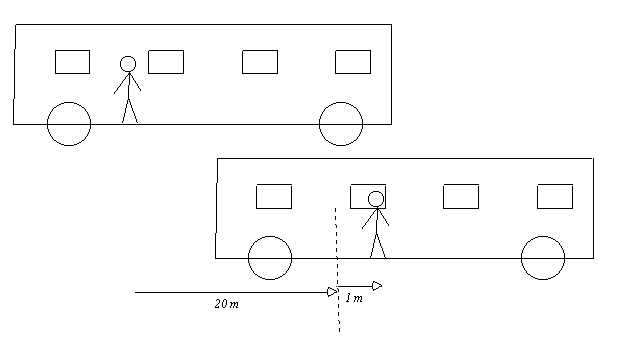
Sur ce schéma, tout se passe en une seconde. Les lignes en pointillé marquent la position du voyageur si il était resté immobile dans le train. Il s'est déplacé de 1 m dans le train, qui s'est lui même déplacé de 20 m. Le déplacement totale du voyageur est donc de 21 m, en 1s.

C'est la loi d'addition des vitesses. A l'inverse si le voyageur marchait dans le sens contraire du train, sa vitesse par rapport à la terre serait 20-1=19 m/s donc dans ce cas on doit soustraire les vitesses. Mais en réalité, on peut dire aussi qu'on les additionnes si on pose que la vitesse du voyageur est négative. Plus précisément on impose un sens positif et un sens négatif pour les vitesses ce qui permet de garder une seule formule pour l'addition des vitesses.

Si le mobile va de gauche à droite, sa vitesse est positive, dans le cas contraire sa vitesse sera négative ce qui permet de garder une seule forme pour la loi d'addition des vitesses: additionner une vitesse négative au lieu de faire une soustraction.